Reciprocal Games I

Tom has built a random generator that is connected to a row of $n$ light bulbs. Whenever the random generator is activated each of the $n$ lights is turned on with the probability of $\frac 1 2$, independently of its former state or the state of the other light bulbs.
While discussing with his friend Jerry how to use his generator, they invent two different games, they call the reciprocal games:
Both games consist of $n$ turns. Each turn is started by choosing a number $k$ randomly between (and including) $1$ and $n$, with equal probability of $\frac 1 n$ for each number, while the possible win for that turn is the reciprocal of $k$, that is $\frac 1 k$.
In game A, Tom activates his random generator once in each turn. If the number of lights turned on is the same as the previously chosen number $k$, Jerry wins and gets $\frac 1 k$, otherwise he will receive nothing for that turn. Jerry’s expected win after playing the total game A consisting of $n$ turns is called $J_A(n)$. For example $J_A(6)=0.39505208$, rounded to $8$ decimal places.
For each turn in game B, after $k$ has been randomly selected, Tom keeps reactivating his random generator until exactly $k$ lights are turned on. After that Jerry takes over and reactivates the random generator until he, too, has generated a pattern with exactly $k$ lights turned on. If this pattern is identical to Tom’s last pattern, Jerry wins and gets $\frac 1 k$, otherwise he will receive nothing. Jerry’s expected win after the total game B consisting of $n$ turns is called $J_B(n)$. For example $J_B(6)=0.43333333$, rounded to $8$ decimal places.
Let $\displaystyle S(m)=\sum_{n=1}^m (J_A(n)+J_B(n))$. For example $S(6)=7.58932292$, rounded to $8$ decimal places.
Find $S(123456789)$, rounded to $8$ decimal places.

This problem actually involves knowledge of combinatorics and probability, and is a bit more complicated than one might initially think.

To solve problems like these, we usually start from the most fundamental part and understand the rule of each game:

1. In game A, Jerry wins if the number of lights turned on is the same as the previously chosen number k. The probability that a given light bulb is turned on is 1/2, so the probability that exactly k light bulbs are turned on is given by the binomial distribution:

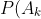&space;=&space;C(n,k)&space;*&space;(1/2)^k&space;*&space;(1/2)^(n-k)&space;=&space;C(n,k)&space;/&space;2^n)

The expected win of Jerry in each round will be:

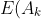&space;=&space;P(A_k)&space;/&space;k&space;=&space;C(n,k)&space;/&space;(k&space;*&space;2^n))

Summing over all possible k, we have the expected win of Jerry in game A as:

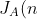&space;=&space;\sum_{k=1}^n&space;E(A_k)&space;=&space;\sum_{k=1}^n&space;\frac&space;{C(n,k)}&space;{k&space;*&space;2^n})

2. For game B, Jerry wins if he manages to generate the same pattern of light bulbs with exactly k lights on as Tom. For a given k, there are C(n,k) possible patterns and the probability for generating a specific pattern is (1/2)^k. Note that the events of Jerry and Tom generating the same pattern are independent, so the winning probability for each round is:

![P(B_k) = [C(n,k) * (1/2)^k]^2 = C(n,k)^2 / 4^n](https://latex.codecogs.com/gif.latex?P(B_k)&space;=&space;[C(n,k)&space;*&space;(1/2)^k]^2&space;=&space;C(n,k)^2&space;/&space;4^n)

The expected win for Jerry in each round will be:

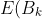&space;=&space;P(B_k)&space;/&space;k&space;=&space;C(n,k)^2&space;/&space;(k&space;*&space;4^n))

Similar to game A, the expected win of Jerry in game B is:

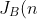&space;=&space;\sum_{k=1}^n&space;E(B_k)&space;=&space;\sum_{k=1}^n&space;\frac&space;{C(n,k)^2}&space;{k&space;*&space;4^n})

3. To calculate S(m), we simply add up all J_A(i) and J_B(i) for i from 1 to m, which could be calculated using formulas above.

The exact calculation for S(123456789) would involve a large scale computation and is unfeasible to be posted here. You would need to write a computer program to perform this. There are more efficient ways to compute the summation using dynamic programming or other algorithmic techniques, but this is beyond the scope of basic mathematics.

More Answers: